
첫 번째 문제입니다. 정답률이 50% 채 되지 않는 3점 문제 치고는 굉장히 어려운 준 킬러 문제입니다. 하지만 막상 문제를 풀어보면 이게 정답률이 이렇게 낮다고? 싶을 정도로 쉬운 문제입니다.

직선 -x=y와 곡선 a^x=y가 만나는 점의 좌표에 관한 문제이기 때문에 일단은 같다고 두겠습니다. 만나는 점의 좌표가 (p, -p)라고 되어있으니 x에 p를 넣어봅시다.
-x=y와 곡선 a^2x=y 역시 만나는 점의 좌표를 (q, -q)라고 되어있습니다. x자리에 역시 q를 넣어봅시다.

이렇게 2개의 식이 나오게 됩니다. 결국 둘 다 밑이 a로 동일하기 때문에, -p와 -q를 곱할 수 있겠습니다.

-p와 -q는 둘 다 음수이기 때문에 곱하면 양수로 나오겠죠? 마지막으로 로그 a의 pq가 -8이라는 사실을 이용해봅시다.

로그의 정의에 의해, a의 -8제곱이, pq라는 사실을 알 수 있습니다.

a의 (p+2q)제곱도 그 결과가 pq이고, a의 (-8)제곱도 그 결과가 pq입니다. 즉, (p+2q)는 -8이라는 사실을 알 수 있습니다.
p+2q=-8 결과적으로 정답은 5번이 됩니다.

두 번째 문제입니다. 문제를 읽어보고 간단하게 정리해봅시다.
일단은 두 함수 y=3^x와 y=log2_x의 y 값을 동일하게 할 수 있는 x값을 구해야 합니다. 그 갯수는 무수히 많을텐데 우리는 그 중 선분 AB가 자연수가 될 수 있는 값을 구할 것 입니다. 선분 AB가 자연수가 되면, 그 후로는 길이를 짧은 순서부터 차례대로 정리할 것 입니다.
그림에서 볼 수 있듯이 log2_x와 m이 만나는 x좌표를 Bm이라고 하고, 3^x와 m이 만나는 x좌표를 Am이라고 부르기로 정해졌습니다.
ㅣ(점 Bm의 x좌표)-(점 Am의 x좌표)ㅣ = 선분 AmBm의 길이가 되겠죠? B-A가 자연수가 되기 위해서는, (자연수 - 자연수)면 되겠네요, 즉 x좌표 두 개가 모두 자연수가 되게 하는 m값을 찾으면 됩니다. (물론 유리수 - 유리수도 자연수가 될 수 있지만, 너무 복잡해짐)

m을 1이라고 가정하면, A1의 값은 0이 되고 (3^0=1), B1의 값은 2가 됩니다. (log2_2=1)
즉, 선분 A1B1의 길이는 2가 되고, 이는 자연수이기 때문에 a1=2가 됩니다. m을 0이라고 가정하지 않는 이유는, 점근선 때문에 3^x=0이라는 근은 아예 존재하지 않기 때문입니다. 0과1사이를 하지 않는 이유는, 유리수 범위까지 생각하면 너무나 복잡해지기 때문입니다.
m을 2이라고 가정해봅시다. log2_4=2이지만, 3^x=2라는 값은, 자연수로는 존재할 수 없기 때문입니다. 그러니 당연히 둘을 뺀다 하더라도 길이가 자연수가 나올 수 없기 때문에 계산 할 필요도 없이 패스하겠습니다.

m을 3이라고 가정해봅시다. A3의 값은 1이 되고 (3^1=3), B3의 값은 8이 됩니다. (log2_8=3) 선분 A3B3의 길이는 7이 되겠고, a2=7이라고 정리할 수 있습니다. 이제 a3만 찾으면 문제 해결이네요,
여기에서, log2_x=m의 경우, m이 자연수이기만 한다면 x역시 무조건 자연수가 나오게 됩니다. 즉, 3^x=m에서 x가 자연수가 나오게 하는 m값을 찾기만 하면 손쉽게 문제를 풀 수 있다는 뜻이죠, 3^x=m에서 x자리에 0,1,2..숫자를 차례대로 대입해봅시다.
3^0=13^1=33^2=9,
0을 넣어서 a1을 구했고, 1을 넣어서 a2를 구했으니, 2를 넣은 m=9라는 값에서 a3를 구할 수 있겠네요.

m을 9라고 가정해보면, 선분 AB의 3번째 자연수 길이가 나오게 됩니다. A9B9의 길이를 a3이라고 둘 수 있겠고, 그 길이는 B9에서 A9를 뺀 510이 되겠습니다. 정답은 510인 5번이 되겠습니다.

세 번째 문제입니다. 로그함수의 특징을 잘 이용합시다. 지금 보면 두 개의 로그함수는 평행이동이 이루어지지 않았기 때문에, 당연하게도 (1, 0)이라는 정점을 지나겠지요? 결국 A의 좌표는 정점인 (1, 0)이 됩니다.
또한 B의 점 역시 너무나 쉽게 구할 수 있는데, B의 좌표는 (4, log2_4)가 되고, log2_4는 결국 2이기 떄문에 B의 좌표는 (4, 2)이 됩니다.

삼각형의 넓이가 2분의 9라고 했는데, 삼각형의 넓이 공식은 밑변x높이x2분의 1입니다. 높이는 4-1인 3이 되고, 밑변은 2-(loga_4)가 됩니다. 정리하자면,

이렇게 loga_4가 -1이라는 것을 구해낼 수 있습니다.

loga_4가 -1이라는 것을 통해, a가 4^(-1)이라는 것 역시 구해낼 수 있습니다. 정답은 4번인 4분의 1!

네 번째 문제입니다. 정답률이 10% 채 안되는 엄청난 킬러문제입니다. 정답률이 낮아 문제가 매우 까다로울 것 같지만 (가)와 (나)의 조건을 적절히 이용하여 문제를 풀 수 있습니다. 솔직히 정답률이 낮아봐야 40%대일 줄 알았는데 생각보다 어려워하는 문제더라구요
일단은 (가)조건을 이용해봅시다.

k^c 와 3^a 양변에 c분의 1 제곱을 곱해주면, k= 3^(c분의 a)라는 결과를 얻을 수 있습니다.

동일한 방법으로 k=5^(c분의 b)라는 결과도 얻을 수 있습니다.


그 외에도 ab에 관한 2개의 식을 만들어 낼 수 있습니다.

그 다음에 (나)조건을 이용하여, 밑이 10으로 같은 로그를 연산해줍니다. (밑이 표기되지 않은 로그는 밑을 10으로 하는 상용로그)
밑이 같은데 결과값도 같으니, 진수끼리의 값 역시 동일하다고 두면 되겠죠? c의 값을 a와 b끼리의 관계식으로 표현이 가능해졌습니다. (가) 조건을 이용하여 문제를 풀어봅시다.

k의 값은 위와 같이 3에 관한 식으로 표현 할 수 있습니다.

k의 값은 또한 5에 관한 식으로도 표현이 가능해집니다.
3과 5에 관한 식, 두가지를 통해 문제를 풀어봅시다.
1. 3에 관한 식으로 문제 풀기

k를 제곱한 뒤, 3에 관한 식도 곱해줘서 정리한 뒤에, 통분을 해 주면 결과적으로 위와 같은 식이 나옵니다.
3의 b분의 a 제곱은 5이기 때문에 결과적으로는, 3x(5^2)이 되는 것이고, 3x25 = 75, 정답은 75가 되겠습니다.
2. 5에 관한 식으로 문제 풀기

역시 동일한 방법으로 문제를 풀었습니다. 2번째 방법이 훨씬 깔끔하고 쉽게 풀리는군요. 어떤 방법을 사용해서 풀어도 답은 75가 나오기 때문에 정답은 당연하게도 75입니다.

다섯 번 째 문제입니다. 솔직히 정답률이 83%이긴 하지만, 그 당시 수학에 조금이라도 자신이 없다면 나형을 선택했던 시절이기 때문에, 가형에는 수학 고인물들밖에 남지 않았다는 점을 고려하면 나형으로 쳤을 때 정답률이 50% 이하대로 나왔을 것 같은 문제입니다.
실제로도 정답률이 50%대 이하였던 1,2번 문제보다 체감상 더욱 어려웠던 문제였습니다.

대충 a의 값을 모르기 때문에, 아무런 지수 함수나 그려줍시다. 대충 1보다 크니까 계형이 이렇게 나오겠죠?

그리고 y=루트3라는 직선을 그려준 뒤, 만나는 점을 A라고 둡시다. y좌표는 당연히 루트3이지만, x좌표를 설정하기가 까다롭기 때문에 문제가 어렵게 느껴졌던 것 입니다.

이와 같이 표시 할 수 있는데, 이 식을 로그로 바꿔봅시다.

바꿔보면, a^x=루트3이라는 식을 만족시키는 x의 값을 구할 수 있습니다. (만족시키는 값 = loga_루트3)
즉, A라는 점의 x좌표에 loga_루트3을 집어넣어주면 되겠죠?

아니면, 로그의 성질을 이용하여 이와 같이 x값을 찾아낼 수도 있습니다.

x좌표도 찾았고, y좌표도 찾았으니, 선분 OA를 그어줍시다. 좌표들을 전부 알고 있으니 두 점을 이용해 선분 OA의 기울기를 구할 수 있겠습니다.

선분 OA의 기울기는 이와 같이 정의됩니다.

선분 AB의 기울기도 마저 정의해줍시다.

선분 AB의 기울기입니다. 선분 OA와 AB가 서로 수직이 되게 하라고 하니, 두 기울기의 곱이 -1이 되면 되겠죠?

둘을 곱해줍시다.

그리고 그 결과가 -1이 되니,

위와 같은 식으로 바꿀 수 있겠네요, loga_루트3을 t로 치환한 뒤 인수분해를 해 줍시다.

위의 식을 인수분해 해 주면

t의 값은 1 or 3, 2개의 값이 나옵니다. (이차함수니까 당연함)
로그함수는 y값의 제한이 없으니 1, 3 두개가 답이 될 수 있겠네요.
여기서 주의할 점은 t값이 1, 3이라는거지, 정답이 1, 3이라는 것이 아닙니다. 1이랑 3을 곱해서 3이라고 답을 내신 뒤, 3번을 찍으시면 바보입니다!

loga_루트3이 1, 3이 되려면, 위와 같은 값이 총 2개 나오게 됩니다.

둘을 곱하라고 했으니, 곱하면 정답은 위와 같이 나오게 됩니다. 정답은 2번!

벌써 마지막 문제네요.. 개인적으로 여섯개의 문제 중 가장 어려운 문제였다고 생각합니다. 3을 기준으로 함수가 달라지기 때문입니다. 지수 함수에 대한 정확한 해석이 요구되는 고난도 문제입니다.

3 이전까지의 함수의 계형입니다. 2^x=y라는 간단한 지수 함수로 되어있기 때문에 충분히 그리실 수 있습니다. 또한, x가 3보다 큰 부분의 함수 역시도, 3을 넣게되면 결국 같은 값을 빼는 것이니 +8만 남게 되므로, 3을 넣었을 때 값이 8이 나오게 됩니다.
0이하의 값을 넣어도 어차피 유리수 값이 나올 것이기 때문에 0이하의 값은 고려하지 않겠습니다. (정수의 개수가 중요)
x의 값이 0부터 3까지 1,2,3,4,5,6,7,8 총 8개의 정수의 값이 나올것입니다.
각각 x의 값이 log2_1, log2_2, log2_3, log2_4,.... log2_8이 될 때마다, y의 값은 정수인 1,2,3,4,...8까지 나오게 되겠죠?
3 이상부터 계산하는 것이 좀 힘들지만 정수인 점의 개수가 23개라는 점을 이용하면 쉽습니다.

이 부분만 제대로 정리해준다면 문제가 쉬워질 것 같습니다.

분수를 없애주면 정리하기 훨씬 편해질 것 같아 위처럼 바꿔주었습니다. 이러한 식에서 x의 값이 커지면 커질수록, 4^-(x+a)라는 값은 결국 0에 가깝게 무한히 감소하게 됩니다.
결국 x의 값이 커질수록 8 - 4^-(3+a)의 값만 남게 되겠죠. 여기서 4^-(3+a)의 값이 1보다 크지 않다면, 아무리 x의 값이 커져 4^-(x+a)라는 값이 0에 가까워진대도, 결국 7 이하로 내려가지 못하기 때문에 23개의 정수가 나올 수 없겠죠? 즉 a는 아무리 커도 -4보다는 작아야 한다는 뜻입니다.
a가 -4가 되면, 4^-(3+a)의 값은 4까지 증가하게 되며, a가 -5가 되면, 4^-(3+a)의 값은 16까지 증가하게 됩니다.
x가 커질수록 4^-(x+a)의 값은 0에 가까워져 결국 점근선은 8-4^-(3+a)가 되겠죠?

4^-(3+a)의 값이 몇인지는 모르지만, 위의 함수에서 정수가 23개가 나왔다는 점을 통해 찾아낼 수 있습니다.

8은 3에서 한 번만 나오기 때문에, 8까지 총 8개의 정수가 나오고, 나머지 부분에서 남은 15개의 정수가 나와야 합니다.
따라서, 아래로 내려가면서 7이 나오면 9개의 정수가 나온 것이고, 6이 나오면 10개의 정수가 나온 것이고, 5가 나오면 11개의 정수가 나온 것이고... 결국 (5-12)가 나오면 (11+12)개의 정수가 나온 것 이죠?
-7까지 나오게 되면 23개의 정수가 나온 것이고, -8까지 포함하게 된다면, 24개의 정수가 나온 것 입니다. 즉, 점근선이 -8보다는 크지만, -7보다는 작은 점에 위치해야합니다.
점근선이 -8에 위치하게 되면, 결국 -8으로 무한하게 다가갈 뿐이지, -8 까지 정수로 카운트하지 않게 되기때문에, 점근선이 -8에 위치하게 되면, 정확히 23개의 정수가 존재하게 되는 것 입니다.

점근선이 -8에 위치하기 위해서는, -4^-(3+a)의 값이 -16이 되어야하며, 결국 4^-(3+a)의 값은 16이 됩니다. -(3+a)의 값이 2이 되야하기 때문에 a는 -5가 됩니다. 정답은 3번!

ㄱ부터 풀어봅시다. 일단 기본적으로 교점에 관한 문제이고, 심지어 로그의 진수자리에 절댓값까지 껴있어서 굉장히 까다로운 문제가 되겠네요.
문제에서 A의 x좌표를 x1, B의 x좌표를 x2라고 두었으니, x좌표들을 구하면 되겠죠?
k의 값이 정해지지 않아서 교점 2개의 위치가 불명확했지만, k를 3으로 놓으면 명확하게 교점이 2개 나오게 됩니다. (A, B)

x의 값이 -1, 2 총 2개가 나오게 되면서, A의 x좌표는 -1, B의 x좌표는 2인 것을 알 수 있습니다.

x1을 -1, x2를 2라고 둔다면, ㄱ은 결과적으로 맞게 됩니다.
이제 ㄴ을 풀어봅시다.

x좌표가 음수인 부분에서 교점 A가 나오고, x좌표가 양수인 부분에서 교점 B가 나오니, 점 A와 B를 절대값이 씌워진 로그를 통해 이렇게 정리 할 수 있습니다.

또한 점 B를 log2_(-x+m)함수를 이용하여, 이렇게도 정리가 가능해집니다. (양수 부분에서 만났으니, 절댓값도 + 붙이기)

마지막으로 점 C를 이와 같이 둘 수 있습니다. (음수 부분에서 만났으니, 절댓값도 - 붙이기)

전부 다 이항해서 빼줍시다. 전부 다 x라고 두면 헷갈리니까 x1, x2, x3로 바꿔주었습니다.
(x1 = A의 x좌표)
(x2 = B의 x좌표)
(x3 = C의 x좌표)

log2_a = 0이 되는 진수값 a는 1이므로 진수에 있는 모든 식이 1이 되야겠지요?

식들의 x1, x2, x3값들을 전부 이항하고, 공통 인수로 묶어줍니다.

결과적으로 이와 같이 정리됩니다. x2(1-k)=-4 와 x3(1-k)=m 식에서 1과 k의 자리만 바꿔주면 값의 부호가 반대가 되니
x2(k-1)=4, x3(k-1)=-m 2개의 식까지 추가로 얻어낼 수 있습니다.

x1, x2, x3를 k,m이 포함된 관계식으로 총 6개의 관계식을 만들어 낼 수 있습니다.
이제 x1과 x3을 곱했을때, x2의 제곱이 나오는 지 확인 해 봅시다.

빨간 동그라미 친 두 개의 식(x1, x3)을 곱해보겠습니다. 참고로 (1+k)는 교환 법칙을 이용하여 (k+1)으로 바꿀 수 있습니다.

두 식을 곱하면 결과가 위처럼 나오게 됩니다. 이제 x2를 제곱해봐야겠죠?

두 개의 식을 곱해보겠습니다. 두 개의 식을 곱하는 것 이지만, 결국 x2곱하기 x2이기 때문에, x2의 제곱이 됩니다.

x1과 x3을 곱했을 때와 결과값이 동일해졌습니다. ㄴ도 맞는 정답이었네요.
마지막으로 ㄷ만 풀어주면 되겠습니다. 일단은 직선 AB와 AC의 기울기를 구해줘야합니다. AB와 AC의 기울기가 같으면서 음양 부호만 다르다면, 합이 0이 되겠죠? AB=-AC라고 두고 풀어줍시다. x좌표는 이미 구해놓았지만, 문자가 2개나 있어서 y좌표를 구하기는 힘들어보입니다.
ㄴ에서 구한 결과인 x1곱하기 x3 = x2^2이라는 것을 통해 a b c의 x좌표 (x1, x2, x3)가 서로 등비수열을 이루는 관계라는 것을 알 수 있습니다.

x2와 x3을 x1에 대한 관계식으로 재정의 할 수 있으며 k와 m의 값에 따라 r의 값이 달라지게 되겠죠?
선분 AB의 기울기를 정의해봅시다.

kx1자체에서 음수가 나오기 때문에 어차피 양수분의 양수로 정의되어, 로그의 진수조건도 충족하게 됩니다.

r과 x1은 둘 다 음수입니다. -r은 결국 양수이기 때문에, 역시나 로그의 진수 조건이충족됩니다. 최종적의로 위의 마지막 식이 선분 AB의 기울기라고 할 수 있겠네요.
이제 선분 AC의 기울기를 정의 해 봅시다.

이와 같이 AC의 기울기가 정의 가능합니다.

둘이 더하면 값이 0이라고 했으니, 위처럼 두면 되겠고, 추가적으로 r^2-1을 합차공식으로 인수분해해줍니다.

그 후, 양변에 x1(r-1)을 곱해주면,

이와 같이 식을 정리 할 수 있겠네요, 제곱하면 어차피 절댓값으로 나오니 r^2를 양수로 두었는데, r 자체는 음수이니, 진수 조건에 부합하기 위해서는 r을 -r으로 고쳐주어야합니다. log2_r이면 진수 조건에 어긋납니다.

값이 0이 되기 위해서는, r이 -1 혹은 -3이어야 합니다. 하지만 공비가 -1이라면 x1, x2, x3이 부호만 다를 뿐, 값은 똑같을 것이고, A와 C의 x좌표가 동일해 질 것입니다. 하지만 그림을 보면 A와 C의 x좌표가 다른 위치에 있는 것을 볼 수 있으므로, r의 값은 -3이 됩니다.
둘의 기울기의 합이 0일 때, 공비가 -3이라는 것이 증명되었습니다.

공비가 -3이니, x1, x2, x3의 관계를 위처럼 정해 줄 수 있습니다. 이제부터 함수에 좌표들을 넣어봅시다.

함수값이 위와 같이 정리되었습니다.

이전에 정리해두었던 곳에 대입해줍시다.

-3x1=x2이므로, 위처럼 두 식이 같다고 둘 수 있습니다.

3k-3 = k+1, 전부 이항하면, 2k-4=0, k=2라는 k의 값을 얻어낼 수 있습니다.
k는 2라는 것이 증명되었고, m값만 구해주면 되겠네요.
k값이 구해졌으니, k에 2를 대입하여 나머지 값도 구해봅시다.

k에 2를 넣게 되면, x1의 값이 -(3분의 4)가 나오게 되며, 결국 공비가 -3인 등비수열이니 나머지 x2와 x3은 4와 -12가 됩니다.

다시 한 번 위의 값을 위 식에 대입한 뒤 풀어줍시다. m의 값만 얻으면 되니, 쉬워보이는 x2에 4를 대입해줍시다.
3분의 m이 결국 4라는 값이 나와야 하기 때문에, m의 값은 12가 나와야 합니다.
k =2, m = 12
k^2+m = 16이므로, ㄷ은 틀렸습니다. 결국 정답은 ㄱ,ㄴ인 3이 되겠네요. 풀이과정이 정말정말정말 깁니다.. ㄱ,ㄴ,ㄷ 세 개를 전부 풀어봐야하니 어쩔 수 없죠..

높은 정답률을 보면 알 수 있듯이, 지수로그함수 중, 굉장히 쉬운 편에 속하는 문제입니다. 그림이 그려져있다고 쫄지 마시고, 그림에서 알 수 있는 정보들을 하나씩 수집합시다. 솔직히 이런 4점짜리 문제는 거저먹는 수준의 난이도의 문제입니다.
함수들의 x좌표와 y좌표값을 주고 있습니다. A, B, C 세개의 좌표부터 설정하러 갑시다.
1. A의 y좌표는 -2이다.

정말 간단하게 A의 x좌표를 구해 낼 수 있습니다. A좌표의 x값을 구해내면, 삼각형의 넓이를 알아 낼 수 있습니다. 높이x밑변을 2로 나눈 값이 삼각형의 넓이가 되는데, 지금 높이가 10에서 A좌표의 x값을 뺀, 8이기 때문입니다.
8을 2로 나누면 4가 나오고 4x선분 BC가 28이 나와야 하니, 선분 BC의 길이는 7이 됩니다. B의 함수값에서 C의 함수값을 빼면 7이 나와야합니다. B와 C의 x 좌표가 주어져 있으므로, 함수값을 구해줍시다.

B에서 C의 함수값을 빼주면 7이 나오므로 관계식을 이용하여 a의 값을 구할 수 있습니다. 그 전에 밑이 다르므로 빼기가 어렵겠네요. 밑 a분의 1을 a로 고쳐줌과 동시에, 로그에 -1을 곱해줍니다.
또한, B의 함수값이 2분의1 loga_9인데, 2분의1을 진수에 올려태워주어 진수값을 3으로 바꿔주겠습니다.

최종적으로 loga_3+loga_8-3이라는 값이 BC의 길이가 되므로, 7이 되어야합니다. 밑이 같은 로그이니 진수끼리 곱해줍니다.
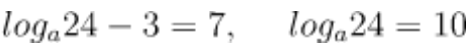
마지막으로 -3을 이항해주면, loga_24=10이라는 식이 최종적으로 만들어집니다. loga_24 = 10을 지수로 고쳐주면,

우리가 구하고 싶었던 것은, a의10제곱이므로, 답은 24가 되겠습니다.

기울기가 -1이고 AB의 길이가 2루트2이니, 1 : 1 : 루트2 직각이등변삼각형이네요. A와 B의 x, y좌표값 차이는 각각 동일하게 2가 되겠네요

또한 a^(x-1)과 log2_(x-1)함수는 둘 다 밑을 a로 하는 함수이고, 진수값과 지수값이 동일하므로, 둘은 역함수 관계에 있습니다. x-1이라는 직선에 대한 원점 대칭 함수이죠.

이런식으로 말이죠. 위의 전체적인 그림을 +x방향으로 1칸만 옮겨주면, x=y라는 직선에 대한 원점 대칭 함수가 됩니다.

함수값에 전체적으로 +1만 해준다면, +x방향으로 한 칸 옮겨주는 효과를 낼 수 있습니다. 점 A의 x좌표를 t라고 두겠습니다.


A와 B의 x,y좌표를 서로 바꾸면 역함수가 됩니다. 즉, A의 x좌표인 t는 B의 y좌표값이고, B의 x좌표인 t+2는 A의 y좌표값인 3-t입니다.
B점은 A의 x좌표를 t라고 두 면, A점과 x좌표의 거리차이가 2이니, 2를 더해준 (t+2)가 됩니다. y값은 3-t와 뺐을 때 2가 나와야하니 1-t가 되어야겠죠?

두 개의 식을 연립해도 되고, 이항 한 후 풀어도 좋습니다. 첫 번째 식을 이항하면 2t = 1이 되니, t는 2분의 1이겠네요.
t의 좌표값은 2분의 1이니, 원래대로 돌려내면 2분의 1 + 1인, 2분의 3이 되겠습니다.

2분의 3을 -x+4에 대입하면 (2분의 5)가 나옵니다. a^(2분의 1) = (2분의 5)이니, a의 값은, (4분의 25)가 됩니다.

B의 y값은 4-(2분의 7) = (2분의 1)입니다. 마지막으로 C의 y좌표는 {0, (a분의 1)}이니, {0, (25분의 4)}가 되겠네요.

세 점의 좌표를 싹 다 구했으니, 삼각형의 넓이만 구해주면 끝! 세 점의 좌표를 알고있으므로, 신발끈 공식이라는 잡기술을 통해 문제를 해결 할 수 있습니다.

위와 같이 점 A B C, 그리고 다시 한 번 점 A의 x, y 좌표를 두고, 사선으로 곱한 뒤 값을 더해줍시다.




그 후 반대로 파란선을 따라 x좌표와 y좌표를 곱한 뒤 더해줍니다.

구한 두 값을 빼줍니다. (넓이니까 절대값 붙이기, 양수로 나옴)

뺀 값에 2분의 1을 곱해주면 삼각형의 넓이가 나옵니다.

마지막으로 삼각형의 넓이의 50배를 하라고 했으니 50까지 곱해주면, 정답은 3x64인, 192이 나옵니다.

일단 첫 번째로, 기울기가 1인 직선이니, 45도의 삼각형이라고 생각하고 문제를 풀어주면 쉽습니다. 기울기가 1이라는 뜻은, C부터 D까지의 x의 변화량과, y의 변화량이 같다는 의미입니다.


이처럼 기울기가 1임을 통해, 두 변의 길이가 같은 직각삼각형이라고 생각하면 문제를 풀기 수월해집니다. 피타고라스 정리를 이용하여 a 값을 알아 낼 수 있기 때문입니다.

이렇게 a의 값을 알아내주시면 문제를 수월하게 풀어낼 수 있을겁니다. 이제 A와 B의 좌표만 구해내주면 수월하게 문제를 풀어 낼 수 있습니다.
a의 값이 6이니, A와 B의 y값 차이는 6인데, 2를 밑으로 하는 지수에서, 값 차이가 6이 되는 것은 2와 8이면 됩니다. A와 B의 값이 각각 2^1과 2^3이라면, 결국 y값의 차이가 6이라는 것이며, x값 역시 6의 차이가 나면 되겠네요.
밑변과 높이를 a로 하는 직각삼각형의 넓이는 6x6을 2로 나눈 값인 18이고, ACDB의 넓이가 30이라고 하니, 나머지 직사각형의 넓이는 12가 되겠네요. 직사각형의 밑변이 6이니, 높이는 자연스럽게 2가 되겠습니다.
즉, A의 y값은 2이고, B의 y값은 8이 되어야겠죠?
결국 A와 B점 모두 x=y 그래프 위에 놓여져 있으므로, (a, a)처럼 x좌표와 y좌표가 동일하기 때문에, (2, 2)와 (8, 8)이라는 점을 지나게 됩니다. x1과 x2 점을 모두 구했네요.

두 식을 연립해주면, 6a = 2가 나오게 되면서, a는 3분의 1이라는 사실을 알 수 있고, 3분의 2 더하기 b가 1이라는 결과를 통해, b값이 3분의 1이라는 사실을 알 수 있습니다.
a= 3분의 1
b= 3분의 1
결국 a+b = 3분의 2가 되겠네요. 정답은 4번입니다.

일단은 함수의 좌표부터 정의해봅시다. 점 A와 B부터 정의하는 것이 좋아 보입니다.

AB의 길이가 8이라는 의미는 B의 y좌표 - A의 y좌표가 8이라는 의미입니다

나중에라도 도움이 될 수 있으니, 미리 준비해놓읍시다. 우리가 주목해야하는 점은 기울기가 -1인 직선입니다.

기울기가 1이니, 밑변과 높이가 동일한 직각삼각형이 되고, 2a^2=8, a=2가 됩니다. 지금 보니 좌표 D도 y값에 0을 대입하여 풀 수 있겠네요.
log2_(x-a)의 x자리에 (a+1)을 대입하면 함수값이 log2_1이 되고, log2_1은 0이니, D의 x좌표는 a+1이라는 것을 알 수 있습니다.

이와 같이 점 D까지 정의했습니다. 우리가 알고싶은 점은 바로 C입니다. C점의 좌표만 알아내도, 나머지를 해결 할 수 있습니다.
C와 B의 x좌표 차이가 2이니, C의 x좌표는 k-2가 되겠네요.

점 ABCD의 좌표를 전부 구해냈습니다. 이제 사각형의 넓이만 구하면 되는데, 삼각형 두개를 쪼갠 뒤 각각의 넓이를 구하고 더하는 방법이 좋아보입니다.
삼각형 ABC의 넓이는 8x2를 2로 나눈 값인 8이 되겠네요. 이제 D와 B의 길이만 구하면 문제가 해결될 것 같습니다. 꼼수를 하나 쓰지면, 아무리봐도 길이가 루트 2일 것 같습니다. D와 B의 x값 차이가 1이고, y값 차이도 눈으로 볼 수 있듯이 x값 차이와 동일해 보입니다. 결정적으로, 밑변이 루트2가 나와야지 곱하면서 루트가 사라져서, 보기에 있는 정답 중 하나가 될 것 같습니다.
즉, 삼각형 BCD는 자연스럽게 넓이가 2가 되면서, 정답은 5번인 10이 되겠네요.
꼼수 없이 푸는 법 입니다.
C의 y좌표값은, B의 y좌표값보다 2만큼 더 큽니다. AB의 y좌표 차이가 8이니, AC의 y좌표 차이는 2만큼 줄어든 6이겠죠? 즉, 선분 AC의 길이가 6이 되고, C의 y좌표 - A의 y좌표가 6이라는 사실을 알 수 있습니다.

2^(k-1)은 8, 2^(k-3)은 2가 되어야지 두 값을 뺐을 때 6이 나오겠죠? 따라서 k의 값은 4입니다.
C의 x좌표값은 자연스럽게 2가 되겠네요
k에 4를 대입하면, A의 y좌표값은 9가 되니, B의 y좌표값은 자동으로 1이 되겠죠? 즉, log2_(4-a)가 1이므로, a는 2가 됩니다.
B의 좌표는 (4, 1)이 되고,D의 좌표는 (3, 0)이 되므로, BD의 길이는 루트 2가 됩니다.
k와 a값을 구했으므로 ABCD의 좌표를 전부 다 구할 수 있습니다.


기울기가 2분의 1인 직선과, 두 개의 로그함수가 만나는 점에 대한 문제입니다. 일단은 기울기가 2분의 1이라는 것을 주었으니, 이 점에 주목해줍시다.

x변화량 분의 y변화량이 2분의 1이니, x축 방향으로 2a만큼 변화했을 때, y축 방향으로는 a만큼만 변화했겠죠? 피타고라스 정리를 통해, 5a^2=20이라는 것을 알 수 있고, a^2=4, a=2라는 사실을 쉽게 파악이 가능합니다.
이제 a의 함수값만 정해주면 되겠네요. a점의 x좌표와 y좌표를 둘 다 모르기 때문에, x좌표를 t로 설정해줍니다.

A라는 점의 좌표를 위와 같이 두었습니다.

B라는 점은 t에 대한 관계식으로 표현 할 수 있습니다.
결국 2+log2_(t+4)에서 1+log2_t를 뺀 값이 2가 나와야겠죠?

+1을 이항하게 되면, 결과적으로 이와 같은 식이 됩니다.

t의 값을 위처럼 구해낼 수 있습니다. A 좌표에 4를 대입하면, A의 y좌표값은 log2_8이 나오고, 그 결과는 3이 됩니다. 이제 삼각형의 넓이만 구해주면 끝나겠네요.

넓이는 이렇게 삼각형을 돌려보면, 밑변은 AC의 길이니 3이 되고, 높이는 A부터 B까지의 x좌표의 차이이기 때문에 구해놓은 2a인 4가 됩니다, 4x3을 2로 나누면 6이 나오므로, 정답은 6이 됩니다.

4점 치고는 정말 쉬운 문제입니다. 헷갈리는 3점 문제보다, 훨씬 명확한 4점 문제가 더욱 쉽습니다. 함수의 좌표들을 한 번 정리해봅시다.
일단은 좌표 B입니다. 2^(-x+a)=y 라는 함수에 0을 대입하면 되므로 (0, 2^a)라는 점이 됩니다. 이제 A라는 점만 구해주면 되는데,
OB = 3OH라는 비례 관계를 일단 알아둡시다. 어차피 O는 원점이어서, 결국 B라는 함수값이, H라는 함수값의 3배이기 때문입니다.
즉, A라는 함수의 값만 찾아내면 된다는 뜻이죠. 상수 a의 값을 정하는 문제이기 때문에, 교점을 통해 구하기는 어려워 보입니다. x자리에 t라는 값을 대입해봅시다.
결국 좌표 A는 (t, 2^(-t+a))가 되고, 3x 2^(-t+a) = 2^a가 됩니다.

위와 같은 식을 통해 t의 값을 구해낼 수 있습니다.

지수 법칙으로 묶인 (-t+a)라는 지수값을 위처럼 분해 후, t의 값을 구해낼 수 있습니다. 그 후, 2^x-1이라는 함수값에 log2_3을 대입해주면,

결국 H라는 함수값은 2가 됩니다. 그렇다면, 이전에 구해두었던 B의 좌표값을통해 상수 a를 구해봅시다.

2^a의 값은 A좌표의 y값의 3배이므로, 6이 됩니다. 즉, a는 log2_6이 되는 것이죠.