오늘은 오도짜세기합해병이 되기위한 두 번째 시간이다. 소수와 합성수를 미리 공부하지 않으면, 이해하기 힘드므로 전 글을 보고오는 것을 추천한다.
https://gragas1.tistory.com/334
[해병 수학] 기열 소수와 짜세 합성수
오늘은 수학을 포기한 젖비린내나는 기열찐빠 앗쎄이들도 올챙이크림내가 펄펄나고 기합넘치는 오도해병으로 거듭나게 해줄 해병 수학시간이다. 수학을 포기했다는 것은, 곧 수학을 두려워한
gragas1.tistory.com
최대공약수에 앞서, 일단 약수에대해 배워본다! 악!!!!
최대공약수란 무엇인가? 일단 약수의 뜻 부터 알아야한다! 일단은 24해병님으로 예시를 들어보겠다.'
24해병님을 만들기 위해, 어떤 해병들이 전우애를 해야하는 가?
3x8 = 246x4 = 2412x2 = 241x24 = 24 등 다양한 방식으로 전우애를 즐길 수 있다.
여기서 24해병님을 만들기 위해 전우애에 참여하는 모든 앗쎄이들을 우리는 약수라고 부른다. 알겠나?
24해병님은 즉, (1, 2, 3, 4, 6, 8, 12, 24) 총 8명의 약수 해병들을 가지고 있는 것이다. 당연한 이야기이지만, 약수가 많으면 많을 수록, 전우애에 참여하는 해병의 숫자가 많으므로, 약수가 많다 = 기합숫자 라는 것을 명심하도록!
약수는 곧 소인수분해와 밀접한 연관이 있으므로, 소인수분해를 실시한다!
앗쎄이! 24 해병님 소인수분해 실시!

악! 4명의 전우들이 서로 물고빠는 모습이 여간 기합이 아니구만!
이렇게 바꾼다면 우리는 약수를 아주 쉽게 구할 수 있게 된다!

2x(2x2x3) = 24이므로, 2는 앗쎄이가 아닌 전우애를 즐길 줄 아는 어엿한 약수-해병으로 거듭났으며, 세 명이 집단 전우애를 즐겨 탄생한 12해병 역시 24 해병님의 약수-해병으로 거듭났다!

처음부터 오도짜세였던 4해병과 6해병 역시 짜세답게 24해병님의 약수였던 것이다.

8과 3해병 역시 24해병의 약수였던 것이다. 이와 같은 방법으로 소인수분해를 통해 약수들을 쉽게 구해낼 수 있는 것이다. 참고로 소인수분해와는 다르게, 1과 자기 자신 역시 약수에 포함하므로, 추가적으로 1해병과 24해병님 그 자체 역시 24해병님의 약수였던 것이었다.
이처럼 약수의 갯수는, 소인수의 갯수에 따라 그 갯수가 달라지게 된다! 약수의 갯수를 한 번 표를 이용하여 구해보자!
오늘 특별히 모신 216 해병님을 통해 약수의 갯수를 구해보겠다. 모두들 영광으로 알도록!!
악! 216해병님 소인수분해 실시!!

| 전우애 실시! | 3 (3) | 3^2 (9) | 3^3 (27) |
| 2 (2) | 3x2 (6) | 3^2x2 (18) | 3^3x2 (54) |
| 2^2 (4) | 2^2x3 (12) | 2^2x3^2 (36) | 2^2x3^3 (108) |
| 2^3 (8) | 2^3x3 (24) | 2^3x3^2 (72) | 2^3x3^3 (216) |
총 15가지의 약수 생성이 가능하며, 이전에는 기열이었지만 이번에만 특별히 1을 어엿한 해병으로서 인정한다면, 1을 추가하여 총 16개의 약수가 생겨나게 되는 것이다!
1,2,3,4,6,8,9,12,18,24,27,36,54,72,108,216 총 16명의 약수 해병들이 존재하는 것을 눈으로 똑똑히 볼 수 있다!
약수의 갯수를 쉽게 구할 수 있는 공식이 있으므로, 관심있는 아쎄이는 직접 확인하도록!

소인수분해 된 소인수들의 거듭제곱에 1을 더한 뒤, 그들을 곱해준다면, 약수의 갯수가 나오게 된다.
3+1 = 4이므로, 4x4=16, 16개의 약수가 나오게 되는 것이다!
다음 숫자의 약수의 갯수를 구해보겠다!
1. 69
2. 892

69해병님을 소인수분해 해보도록! 전 글과 똑같은 결과가 나오게 된다! 거듭제곱이 없다고 하지 말고, 주의깊게 보도록!

그렇다! 3해병과 23해병은 거듭제곱이 없는 것이 아닌, 쓸 필요가 없어서 쓰지 않고있던 것 이었다!

각 각을 1으로 인정하게 되면, 1+1 = 2이므로, 2x2 = 4 총 4개의 약수가 나오게 된다!
1,3,23,69 얼마나 기합스러운가!
892해병 역시 동일한 방식으로 약수의 갯수를 구할 수 있다!

거듭 제곱에 1씩 더한다 실시!
(2+1)x(1+1) = 3x2 = 6,
즉 892해병님의 약수 갯수는 6개가 된다!
1,2,4,223,446,892
이제 약수에 대해 어느정도 감을 잡은 것 같군. 그렇다면 최대공약수란 무엇인가??
"두 숫자 사이에 공통되는 약수 중 가장 큰 약 수" 라는 뜻 이다!
74해병님과 892해병님을 예로 들어보자!
1,2,37,74
1,2,4,223,446,892
각 각 74해병님과 892해병님의 약수들이다! 이 중 두 해병님들과 공통적으로 전우애를 즐기는 오도해병이 보이는가??
그렇다 바로 1해병과 2해병이다! 참고로 1해병님은 "어떠한 해병들과도 항상 전우애를 즐기는 오도짜세기합숫자"이므로 해병대에 입대하기 전 1해병님을 정신을 이어받도록!
어찌되었든, 공통적으로 전우애를 즐기는 오도해병 중, 가장 큰 숫자를 바로 최대공약수라고 한다!
그렇다면, 어떻게 해야 공약수들을 구할 수 있을까??
이제부터 216해병과 243해병님 사이의 공약수들을 구해보겠다! 앗쎄이 원 위치 후 집중!
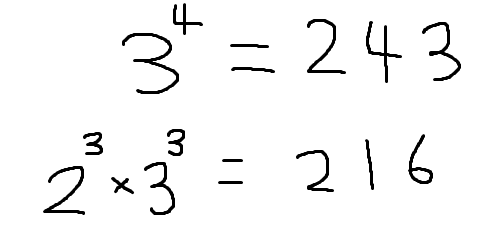
소인수 분해는 필수다! 일단은 공통적으로 3해병이 여기저기 난잡하게 껴있는 것을 확인 할 수 있다!
거듭제곱따윈 무시하고 이를 한 번 해병식으로 풀어 써 보겠다.

이로써 공약수를 구하기 훨씬 편해졌다!
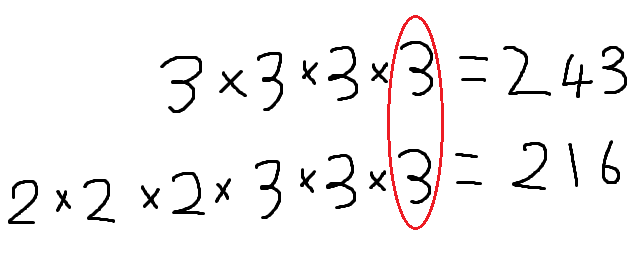
3이 동일하게 전우애를 즐기고 있으므로, 3.. 새끼.. 공약수!

3x3인 9 해병 역시 동일하게 두 곳에서 전우애를 즐기고 있으므로, 9.. 새끼.. 공약수!

3x3x3인 27 해병 역시 동일하게 두 곳에서 전우애를 즐기고 있으므로, 27.. 새끼.. 공약수!!
그 외에는 어느 곳에서나 전우애를 즐기고 계신 오도짜세 1해병님까지!
1,3,9,27 총 4개의 공약수가 존재한다! 그 중 가장 큰 숫자는 27이므로, 최대공약수는 27이 된다!
전우애 도중 최소공배수에 대해 알아본다! 실시!!
배수 역시 먼저 학습이 필요하지만.. 굳이 왜 배워야하지 모르겠다!
3의 배수 = 3,6,9,12,15,18..
3x1 3x2 3x3 3x4 3x5 3x6...
5의 배수 = 5,10,15,20,25,30....
5x1 5x2 5x3 5x4 5x5 5x6
설명은 견쌍섭 해병님이 긴빠이했으므로 알아서 악으로 깡으로 이해하도록!!
그렇다면 공베수에 대해 알아보겠다!!
두 숫자간의 배수 중, 공통적으로 존재하는 해병, 그것이 곧 공배수이다!
2와 4의 배수를 각 각 살펴보겠다!
2의 배수 = 2, 4, 6, 8, 10, 12
4의 배수 = 4, 8, 12, 16, 20, 24...
공통적으로 껴있는 해병들이 보이는가?? 그렇다. 2의 배수 사이 사이에 4의 배수들이 전부 껴있으므로, 4의 배수 전체가 공배수가 되어 버린다!
왜 이렇게 되냐면, 4라는 숫자가 이미 2의 배수 중 하나이기 때문이다. 2의 배수인 6,8,10과 2의 공배수 역시 각 각 6,8,10의 배수 전체가 되어버린다!
다른 케이스를 보자!
3과 5의 배수를 각 각 살펴보겠다!
3의 배수 = 3, 6, 9 ,12, 15, 18, 24 ,27, 30...
5의 배수 = 5, 10, 15, 20, 25, 30...
공통된 해병들이 보이는가? 그렇다 15의 배수인 15, 30, 45, 60 등이 3과 5의 공배수들이 되는 것이다!
3x5 = 5x3과 동일하기 때문에 15의 배수가 공배수가 되는 것이다!
3과 5는 아무런 연관이 없는 해병들이다. 이 둘의 관계를 서로소라고 부른다!
서로소는 두 수 간의 공약수가 1밖에 존재하지 않는 변왕추, 쾌흥태 해병간의 관계처럼 서로가 서로를 증오하는 관계라고 할 수 있다!
이러한 서로소끼리의 공약수는 간단하게 두 서로소를 곱한 짜세합성수의 배수가 두 수간의 공배수가 되는 것이다.
그렇다면 짜세 숫자인 6과 9처럼 서로소도 아니며, 배수에 포함되는 관계도 아닌 두 수간의 공배수는 어떻게 구할까?
6의 배수 = 6, 12, 18, 24, 30, 36, 42, 48, 54
9의 배수 = 9, 18, 27, 36, 45, 54
6은 두 수를 간격으로 공배수가 나오고, 9는 한 수를 간격으로 공배수가 나온다! 이 두 수간의 공배수를 구하기 위해선 소인수분해가 필요하다!
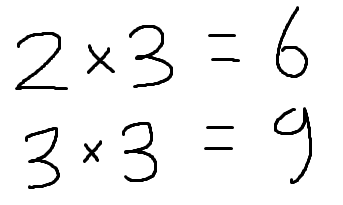
두 곳에서 전우애를 즐기는 공약수 해병 (3)이 존재하고, 서로소 해병 (2와 3)이 각 각 존재하는 것을 볼 수 있다! 서로소는 서로 곱하면 공배수가 되므로 곱하도록! (2x3) = 6
또한 공약수인 3은 공약수이므로, 그대로 위의 6에다가 곱해주면, 6x3 = 18, 즉 18의 배수가 공배수들이 된다는 것을 알 수 있다! 이 행위가 귀찮다면 직접 배수들을 써보고 비교해보며 공약수를 찾는, 해병-귀납법을 이용하여 찾을 수도 있으므로, 각 각 선호하는 방법을 이용하도록!
이로써 배수에 포함되는 관계, 서로소 관계, 동일한 해병이 곱해져있는 관계 등 모든 숫자 사이에서 사용할 수 있는 최소공배수 구하기를 알아보겠다!
1. 구하고자 하는 두 해병을 소인수분해시킨다!
2. 두 수 간의 각 각 다른 기열-서로소해병이 존재하면, 모두 전우애 실시!
3. 두 수 간 공통되는 기합-공통소인수해병이 존재하면, 공통소인수해병까지 전부 전우애시킨다!
아래의 썅내나는 예시를 보고 알아서 잘 이해하도록!
24해병과 28해병간의 해병-최대공배수를 구해보겠다.

아쎄이! 소인수분해 실시!!!!!
공통되는 소인수해병이 보이는가? 그렇다 바로 2의 제곱인 4해병이 떼씹전우애를 즐기고 있었다.

남아있는 기열놈들을 전부 곱해주자! 2x3x7.. 아뿔싸! 이 정도 수준의 곱셈은 해병-필즈상이 걸린 해병 난제에 해당되므로 1q2w3e4r! 해병님의 도움을 받아야한다! 그 결과, 42라는 답을 도출해낼 수 있다!
이제 기합 해병인 4 해병님을 전우애시켜주어야 하는데, 두 숫자에 공통적으로 존재하므로, 두 번 곱하지 말고 한 번 곱해주어야한다!!
42x4 = 168이므로, 해병-최소공배수는 168이 나오게 된다!
배웠으면 문제를 풀어보고 해병 공약수, 공배수 수업을 마치겠다!
74와 892해병님의 최소공배수를 구해보아라!
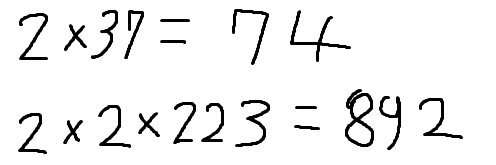
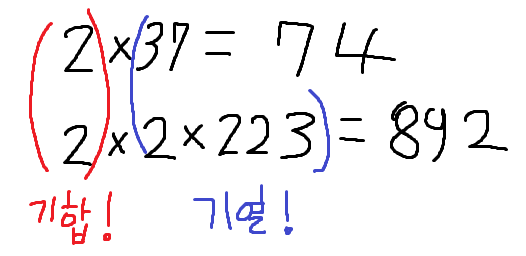
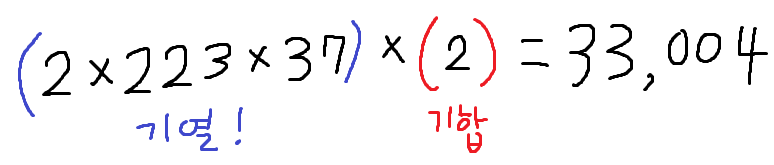
기열 x 기합 = 해병-최소공배수 공식을 잊지 말도록!